Trepando las dimensiones
Basado en un artículo de Jaime Poniachik
La novela Flatland, escrita en 1884 por el inglés Edwin A. Abbot recrea la fantasía de un mundo plano, de dos dimensiones. Las criaturas de ese universo son chatas, sin espesor, y se deslizan sobre la superficie sin poder alzarse nunca de ella.
No es difícil imaginarse una realidad bidimensional. Una ameba colocada sobre una superficie chata es esencialmente bidimensional, su búsqueda de comida a través de pseudópodos se realiza en el contorno bidimensional, y no hacia arriba o hacia abajo.
Así como existe un mundo tridimensional (el nuestro) y también el mundo de dos dimensiones de las amebas (o de Flatland), podemos suponer la existencia de un mundo de cuatro dimensiones espaciales.
El misterio del cuarto amarillo
En “El misterio del cuarto amarillo”, el maestro del suspense, Gastón Leroux (autor de “El Fantasma de la Ópera”), propone el siguiente enigma: El cuerpo de una dama que ha sido atacada es encontrado en un cuarto herméticamente cerrado por dentro. Un misterio similar es propuesto por Edgar A. Poe en su relato “Los crímenes de la Calle Morgue”. En ambos casos, los autores entregan explicaciones plausibles sobre la forma en que se ejecutó el crimen.
Un ser tridimensional podría ejecutar un crimen perfecto en un mundo bidimensional, uno que ni siquiera Poe o Leroux podrían explicar.
En un universo bidimensional, un cuarto herméticamente cerrado podría ser, sencillamente, un rectángulo. Ninguna criatura de dos dimensiones podría entrar en esta habitación sin abrir un boquete en el perímetro del rectángulo.
Pero un asesino tridimensional, podría fácilmente salirse del plano, ingresar al cuarto, cometer el asesinato y volver a salir del cuarto sin dejar huellas.
En forma análoga, un asesino de la cuarta dimensión podría entrar y salir de un cuarto tridimensional perfectamente cerrado sin tener que tocar ni paredes ni techo.
Espiando el hiperespacio
Qué aspecto tienen los objetos de cuatro dimensiones? Eric Temple Bell, autor inglés de libros de historia de la ciencia, advirtió que “nadie que esté fuera de un asilo de locos puede representarse un espacio de cuatro dimensiones”. Este sitio es, entonces, el lugar justo para intentarlo. Como objeto representativo elegiremos el hipercubo.
Para llegar al hipercubo vamos a ir explorando figuras análogas de un mundo de menos dimensiones. Comenzamos con el cuadrado. El cuadrado es una figura plana, o sea, de dos dimensiones. Podemos construirlo a partir de figuras de una dimensión. Si tomamos un segmento de digamos, un metro de largo y lo unimos con otro segmento paralelo de igual longitud, podemos armar el cuadrado uniendo los vértices correspondientes de ambos segmentos. Partiendo de dos elementos que pertenecen a universos unidimensionales (los segmentos) hemos conseguido construir una figura bidimensional (el cuadrado). Se puede decir que el cuadrado conecta a dos universos unidimensionales paralelos. Ver figura 1.
 Figura 1 – El cuadrado, formado conectando dos segmentos unidimensionales
Figura 1 – El cuadrado, formado conectando dos segmentos unidimensionales
Para pasar de un mundo de dos dimensiones a uno tridimensional, utilizamos un procedimiento similar. Dibujamos un cuadrado en un plano y otro cuadrado en un plano paralelo, uniendo los cuatro vértices del primer cuadrado con los cuatro correspondientes del segundo, obtenemos un cubo como se muestra en la figura 2.

Figura 2 – El cuadrado, construido conectando dos cuadrados bidimensionales
Imaginemos ahora un cubo flotando en el espacio tridimensional, y otro cubo igual flotando en un espacio tridimensional paralelo. Si conectamos los ocho vértices del primer cubo con los vértices correspondientes del cubo en el universo paralelo, obtenemos un hipercubo.
La representación de un hipercubo es la parte más problemática. Una representación posible del hipercubo se muestra en la figura 3. Si pudiéramos ver cuatro dimensiones, todas las aristas del hipercubo serían ortogonales entre sí, como lo son en el cuadrado y en el cubo. Hemos hecho un salto doble, del hipercubo de cuatro dimensiones a una representación en perspectiva de sólo dos dimensiones sobre la pantalla.
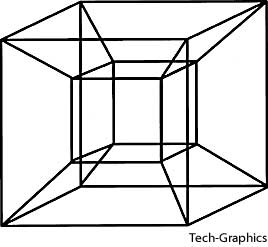
Figura 3 – El hipercubo de cuatro dimensiones (tesseract), construido conectando dos cubos tridimensionales.
Contando vértices, aristas, y…
Un cuadrado posee una única cara, cuatro vértices y cuatro aristas.
El cubo, que posee una dimensión mas, tiene seis caras, ocho vértices y doce aristas.
En la tabla siguiente se resumen los datos de vértices, aristas, caras y cuerpos contenidos en un punto, segmento, cuadrado, cubo, hasta llegar al hipercubo. O sea, partimos de la figura sin dimensión (el punto), pasamos por la figura unidimensional (el segmento) y vamos trepando las dimensiones hasta llegar al hipercubo. Según algunos autores, hipercubo es todo cubo que tenga más de 3 dimensiones. El cubo de 4 dimensiones tiene su nombre propio: tesseract.
|
Vértices |
Aristas |
Caras |
Cuerpos |
|
| Punto |
1 |
- |
- |
- |
| Segmento |
2 |
1 |
- |
- |
| Cuadrado |
4 |
4 |
1 |
- |
| Cubo |
8 |
12 |
6 |
1 |
| Tesseract |
16 |
32 |
24 |
8 |
Tabla 1 – Cantidad de elementos de cada figura geométrica
La cantidad de vértices de cada figura sigue una ley exponencial simple, una potencia de dos. Para el tesseract, es 2 elevado a la cuarta potencia, o sea 16. El cálculo de los otros elementos (aristas, caras, etc.) sigue leyes un poco más complicadas.














