El juego de la vida de Conway
Extractado de Wikipedia, contiene ejemplos del juego agregados por "La Botica"
Una de las consecuencias de la accesibilidad de las computadoras es la capacidad de correr simulaciones en casa. Las simulaciones pueden ser desde una simple recreación, hasta una poderosa herramienta para comprender nuestro Universo. Una de las razones por las cuales se construyen supercomputadoras cada vez más potentes, es su capacidad de simulación de sistemas climáticos, reacciones nucleares, simulaciones moleculares, etc.
Una de las primeras simulaciones en aparecer en el mundo de la computación es el juego de la Vida de Conway. El juego de la vida es el mejor ejemplo de un autómata celular, diseñado por el matemático británico John Horton Conway.
Hizo su primera aparición pública en el número de octubre de 1970 de la revista Scientific American, en la columna de juegos matemáticos de Martin Gardner. Desde un punto de vista teórico, es interesante porque es equivalente a una máquina universal de Turing, es decir, todo lo que se puede computar algorítmicamente se puede computar en el juego de la vida.
Desde su publicación, ha atraído mucho interés debido a la gran variabilidad de la evolución de los patrones que genera. Se considera que la vida es un buen ejemplo de emergencia
y autoorganización. Es interesante para los científicos, matemáticos, economistas y otros observar cómo patrones complejos pueden provenir de la implementación de reglas muy sencillas.
El juego de la vida es en realidad un juego de cero jugadores, lo que quiere decir que su evolución está determinada por el estado inicial y no necesita ninguna entrada de datos posterior. El “tablero de juego” es una malla formada por cuadrados (“células”) que se extiende por el infinito en todas las direcciones. Cada célula tiene 8 células vecinas, que son las que están próximas a ella, incluso en las diagonales. Las células tienen dos estados: están “vivas” o “muertas” (o “encendidas” y “apagadas”). El estado de la malla evoluciona a lo largo de unidades de tiempo discretas (se podría decir que por turnos). El estado de todas las células se tiene en cuenta para calcular el estado de las mismas al turno siguiente. Todas las células se actualizan simultáneamente.
Las transiciones dependen del número de células vecinas vivas:
- Una célula muerta con exactamente 3 células vecinas vivas “nace” (al turno siguiente estará viva).
- Una célula viva con 2 ó 3 células vecinas vivas sigue viva, en otro caso muere o permanece muerta (por “soledad” o “superpoblación”).
Ejemplos de patrones
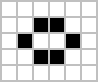
Existen numerosos tipos de patrones que pueden tener lugar en el juego de la vida, como patrones estáticos (“vidas estáticas“, en inglés still lifes), patrones recurrentes (“osciladores“, oscillators, un conjunto de vidas estáticas) y patrones que se trasladan por el tablero (“naves espaciales“, spaceships). Los ejemplos más simples de estas tres clases de patrones se muestran abajo. Las células vivas se muestran en negro y las muertas en blanco.
|
|
|
||||||||||||||||||||||||||
Programas para el Juego de la Vida
Se encuentran disponibles muchísimos programas, tanto en línea como disponibles para ser bajados, que corren el Juego de la Vida con sus reglas originales y variaciones. Para más datos, se recomienda consultar los links de Wikipedia, en español y en inglés:
http://es.wikipedia.org/wiki/Juego_de_la_vida
http://en.wikipedia.org/wiki/Conway’s_Game_of_Life
Ejemplos de "La Botica"
De entre los programas disponibles utilicé éste:
http://www.granvino.com/jam/stuff/juegos/gamoliyas/spanish/index.htm
Una de las ventajas de este programa es su sencillez. Además, está en español, informa la población de la simulación y si ha entrado en un estado estable, y permite guardar y cargar tableros. A continuación varios tableros que hice en el programa (Al cliquear en la entrada se abrirá la simulación, lista para correr, en una ventana nueva):
Transbordador (es interesante analizar qué función cumplen los bloques cuadrados en los dos extremos)
Pistola de planeadores (atención a ésta, que es muy interesante!, y que está basada en dos transbordadores en colisión)
A partir de estos ejemplos, quedan incontables desafíos para el lector: Encontrar osciladores distintos de aquellos mostrados, o con períodos más largos, patrones de continua expansión, explorar choques entre naves y planeadores, o entre naves y patrones estáticos, etc.
En estos dos lugares encontrarán muchísimos ejemplos más:
Wiki del juego de la vida
Noticias y recursos para el juego de la
vida
Como otra alternativa para explorar el Juego de la Vida, se puede jugar una simulación de guerra, donde comandamos una facción, la computadora es el enemigo, y el objetivo, obviamente, es conquistar el tablero.
El juego se encuentra disponible en:
http://www.ctrl-alt-dev.nl/Projects/LifeAsWar/LifeAsWar.html
En la página podrán ver también un video en youtube que contiene un corto tutorial con la estrategia para ganar el juego.